ОБЩИЕ ДАННЫЕ САМОЛЕТОВ

Приложение А

A. I. ОБЩИЕ ДАННЫЕ САМОЛЕТОВ, ИСПОЛЬЗОВАННЫЕ
ДЛЯ РАСЧЕТОВ В РАЗЛИЧНЫХ ПРИМЕРАХ, И КОЭФФИЦИЕНТЫ
УРАВНЕНИИ ПРОДОЛЬНОГО ДВИЖЕНИЯ

, Для расчетов использовались данные пяти самолетов различ­ных типов. Ниже приводятся эти данные и результаты расчетов коэффициентов уравнений продольного движения. і Самолет Ml — тяжелый транспортный самолет с прямым крылом. Режим полета: */g = 8000 м, 14=650 км/час, Л1=0,585, р<>=0,05354 кГ ■ сек2 • мг4.

Самолет М2 — истребитель со стреловидным крылом. Режим полета: t/g=10000 м 1/е=860 км/час, М=0,832, ре=0,04206 кГх X сек2 • м~*.

Самолет М3 — тяжелый бомбардировщик со стреловидным крылом. Режим полета: #g=1000 м, 14=700 км/час, Л1=0,578, ре=0,1134 кГ • сек2 • м~*.

Самолет М 4 — средний пассажирский самолет с прямым крылом. Режим полета: t/g=1000 м, 14=288 км/час, М=0,24, ре=0,1134 кГ • сек2 • м~4.

Самолет М 5 — тяжелый пассажирский самолет со стреловид­ным крылом. Режим полета: i/g = 2900 м, 14=700 км/час, М=0,6, Ре=0,09272 кГ • см2 • м~4.

Коэффициенты уравнений продольного движения сведены в табл. А.1.

Таблица A. I

Коэффициент	Самолет М 1	Самолет >1 2	Самолет М 3	Самолет № 4	Самолет №•5
аЬ	0,171	0,171	0,171	0,171	0,171
а. X	0,00724	0,035	—	—	—

Коэффициент	Самолет № 1	Самолет № 2	Самолет >3 3	Самолет Мк 4	Самолет М 5
а.	0,0268	0,0197
У
аУ	—	— .	—	—	—
«8	—	—	—	—	—
	0	0,056	0	0	0
ь.	0,13	0,056	_	_	___
X
Ь.	0,731	1,13	1,39	1,61	1,15
У
ЬУ	—■	—1	•—	—	—-
h	—	—	—	—	—
*3	—	—	—	0,323	—
сь	0,676	1,28	1» 14	1,65	0,94
с.	0,00567	—		_	_
X
с.	0,637	7,51	1,94	3,23	0,97
У
с..	0,104	0,0556	0,13	0,427	0,12
У с8	2,41	13,2	4,72	5,4	3,18
*3				0,538

Примечание. В табл. А.1 даны значения коэффициентов, при ко­торых углы в уравнениях движения измеряются не радианами, а градуса­ми; в этом случае коэффициент при первом члене второго уравнения (2.10) или первого уравнения (2.11) должен быть записан в форме V*/57,3.

Сведения о передаточных числах автопилота приведены в табл. А.2.

Таблица А.2 Передаточное число Самолет № 1 Самолет № 2 ..Самолет Ms 3 Самолет *й 4 Самолет № 5 1.2 1,0 2,0 1,0 2,0 /. в сек а 0,93 0,3 0,4 0 . 1.3 1у в град(м 0,07 0 0 0 0,08

В формуле (3.1): &i—ax “Ь^у V* а2=а-хЬ-у —а-уЬ-х + сь(ах —b-y)—Vе{ахс-у аг=Ч{Нсу-с-х)—съ{ахЬ-у +ау b-x)+V е{а-хс-у +а;с-), а*=Ч(Ьхс> ~bycxl

b*=bxCj-c-x, j bi=b-xc-y-b-cx. j В формуле (3.2): сй~ах> ci=aibi+aibi +aiK+cy^)> = + +ayh) + Ve(axCy +ayci)- В формуле (3.3): J di=bic*+cxVe — j В формуле (3.4): eo=bi» ei *=ЬЛЧ+СЇУ*1 e*=V t{b’xC’y—b’ycx). В формуле (3.7): fo~cy byCy’ ) fi=aiCi-a-ci-c~(aJcb-y+a>bi). j В формуле (3.8): go=<*-y, gi=&yi4+cfVJ, ■ ёя=аь(с-у — byCy).

А.2. ВЫРАЖЕНИЯ ДЛЯ КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ, ОПРЕДЕЛЯЮЩИХ ПАРАМЕТРЫ ПРОДОЛЬНОГО ДВИЖЕНИЯ ПРИ ВОЗДЕЙСТВИИ ПОРЫВОВ ВЕТРА

(Al> (A. 2)

(v4.3)

(AA)

(Л.5)

(Л.6)

(Л.7)

 

В формуле (3.9):

^о~Ьу»

hl=axby +aybi + ЬуЧ + Су Ve<

h2=<?і(«і+ a — (a — с — + a — cx).

В формуле (3.10):

*o ~byt

h—axb’y ^~aybx ~^~Ь’у (Cb^rCy’VX

h=(H+cy Ve) К *y +1®y )•

В формуле (3.13):

a~b’y H~cy Ve~bc»)> I

^2 = Ьу ci ~b Cy Уе> j
b0 = biCy~Cx> J

b=bxCy-byCx>

В формуле (3.14):

rfo=rfo=^. j

d =*4^bx4+c-xV t. j

l) формуле (3.15):

ео=ео=Ьх*

6y^r=C — b’x (c£ — f-Су lfg),

e2T*e2=Ve(bxc-y-byc-x).

В формуле (3.17):

Л-/»=^-*р<у-

В формуле (3.18):

A0"=A) = *y-

В формуле (3.19):

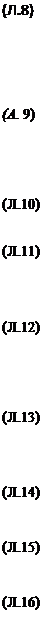>о = k = by* ri = Ьу b Cy Ve)

В формуле (3.22):

y’o=Vy-ci* Л=с — b-x — с-хЬу, Л=-^с( + ьу + сз+суVe+г&>

k2=a^b — — j — и у b-x -|- ifl’x л^с^У/ е-^-с^/ ei

кз~аЛсх +^icy)+(ai^y ‘~aybx)(cbJrС8г»)+

+ сьН («і + *y)++ «у «і).

К—=ЧІРхсу ~byc±)+b — cbiyVe+cJb{axby + a• bx),

*5=К ^ + a* **) — «Л <Vy В формуле (3.23):

/o=ai>

ll = axby ~~aybx ~~а’х(.Ч^~Су^е~~

/2 = «6(^Cy—Ci) + («Jr^ +ayftir) (4 + CA) +

+ <W» + V. («І <?> + Ay ^ ),

h = 4(bkCy-byC-x)+ СЛ («і by + ay bX )•

В формуле (3.24):

щ=ьх,

ml—bx(Cb^~ Cfa “Ь C—V

Щ = ЬХСЛ +Ve(biCy — byCx)-

В формуле (3.25):

n0=c-y-byc-y.,

ni=aici +ayci~cy(aiby +aybi)>

n2— by Cfiy,

*3 = сМа’хЬу +aybi)- В формуле (3.26):

Яо~ау>

Я—ау (С»+Су^+<У&)»

-by су) + ау cih> Яз = аьЬу *Vv

sn=-"b-с—с-. 0 ху х» S, = £• &• —£• 6* . 1 у jr дг у * В формуле (3.29): Uq = # , щ=ахЬу —ayb-x —а-х (c^Cy-V е—сьц), Щ=(ах Ьу +aybi) (с* + с6%)с~ — ~ci)+ve(aicy +л-, С’х)+а’хсьіь, «з=^(йіс — +<*•&;). В формуле (3.30): vi=bi (4—cyVe+^M ®2=V«** + Ve(bxcy —cxby). В формуле (3.31): • Щ=cy —bxc у • +a-yci ~Cy<aiby +a-ybJc)- В формуле (3.32): •^0^=®у * (Cf + CjV^ + Cj/j), ■*2 = а* (С’у — h Су) + % СЬ V

(Л.24)

(Л.25)

(Л.26)

(Л.27)

(Л.28)

 

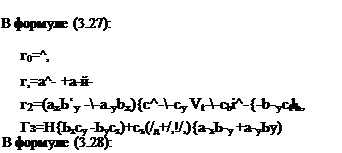В формуле (3.33):

Уо—b’y >

У=ахьу +<>-yh +by {Ч+с-‘У’+с^

y2=(<*iby +а — **)+^cth,

У a=в* (*i «*-*;«*)+* А (аі + ау Ь* )•

В формуле (3.34):

*o=V

*і—*; (**+<^в+<?,/*),

*ї=Ь. усьіь,

*з=byCjq

4i=by +^+^Ve+cs tj,

?2=(<*+*« *’»)+ <> V/, + c5 /в,

?3~Ci(by

<P4=V*V

Приложение В

В.1. РАСЧЕТ ИНЕРЦИОННЫХ КОЭФФИЦИЕНТОВ И ПЕРВОЙ ФОРМЫ
ИЗГИБНЫХ КОЛЕБАНИИ КРЫЛА

В соответствии с общей формулой (3.91) получаем следующие выражения для инерционных коэффициентов в уравнениях (3.101):

Мц = т —масса самолета;

Afi2=Af2i=0—вследствие ортогональности первой и второй обобщенных координат;

Ц 2 т

М13=МВ1=2 f т’ (<z1)%{zl)dzl—2’^i тк(г1к)?(г1к)4 •

0 А=1

где > г,— координата данного сечения крыла в осях, свя­

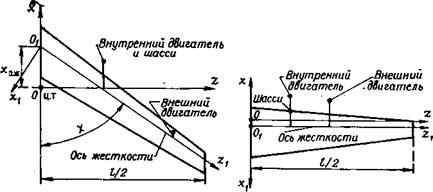
занных с осью жесткости (рис. В.1 и В.2); /,=//cos х— размах крыла по оси жесткости;

X—угол стреловидности по оси жесткости; т’ (г,)—.масса крыла на единицу длины по оси жест* кости;

£ (2,)— первая нормальная форма изгибных колебаний крьґла, отнесенная к вертикальному перемеще­нию его конца;

mK(ziK)—масса нагрузки на крыле, сосредоточенной в точке с координатой ziK (двигатели, шасси); M<n~Iz—момент инерции самолета относительно оси z;

1,/2

^23=^32= — 2 j (*о. ж-{-*1ц. тsinх+-*т. тCOSyOU^i)m'{zl)dzl — о

m

-2 2 (^о. ж+гг1к8Іпх + ^ікС08х)/ик(гік)5(г1к),

ft=l

где ЛГ0.ж— расстояние между центром тяжести и точкой

пересечения оси жесткости крыла с корневой хор­дой (положительное, если центр тяжести лежит впереди упругой оси);

zi„.t— координаты центра тяжести секций крыла в си­стеме осей Xz-,

jc1k, zlK— координаты сосредоточенных нагрузок,

Z./2 т

Мзз=2 J ТГЇ (Zj) $2 (z,) rfz, — f 2 2 тк (zlK) ? (ziK).

О ft=l

Рис. В.1. Геометрические соотношения Рис. В.2. Геометрические соотно — для стреловидного крыла шения для прямого крыла

Для вычисления нормальных форм и частот упругих колеба­ний крыла или других частей самолета существует значительное число приближенных методов. В основу большинства из этих методов положено уравнение (3.87), которое для этих целей записывается в форме

й дТ ■ Ш 0

At dqt dqi

Подробное описание указанных методов можно найти, напри­мер, в монографии [39].

Для расчета первой нормальной формы только изгибных де­формаций крыла, а также для расчета инерционных коэффици­ентов по приведенным выше формулам необходимо иметь сле­дующие данные:

а) некоторые характеристики самолета;

б) геометрию крыла и положение его оси жесткости;

в) жесткость крыла на изгиб по размаху;

г) распределение массы по размаху;

д) положение центра тяжести каждой из секций крыла, на которые оно разбивается для расчета;

е) массы сосредоточенных нагрузок крыла и координаты то­чек их приложения.

Часть данных по самолетам № 1 и № 3 приведена в «Прило­жении А». Дополнительные данные по п. «а» и данные по осталь­ным пунктам приводятся ниже.

а) Характеристики самолета.

Стреловидность крыла по оси жесткости:

самолет № 1 х=^°>

самолет № 3 х=39°.

Расстояние между центром тяжести и точкой пересечения оси жесткости крыла с корневой хордой:

самолет № 1 хо. ж=0,8 м,

самолет № 3 х0.ж=—4,45 м.

б) Геометрия крыла самолетов № 1 и № 3 показана на рис. В.1 и В.2.

Данные по пп. «в», «г» и «д» приведены в табл. В.1.

Таблица В.1 2 гх EI кГ-м~2 т’ to) кГ-сек’-мГ1 X — L ц. т h № 1 № 3 № 1 № 3 № 1 М 3 0.0 47,9-106 38,1-10® 29,2 68,0 0,049 —0,300 0,1 42,6-10® 31,5-10® 32,3 83,6 0,165 0,132 0,2 32,6-106 25,4-10* 31,4 52,4 0,145 0,256 0,3 23,4-10® 18,5-10® 87,0 53,8 0,051 0,260 0,4 16,0-10® 13,1-10® 73,3 56,2 0,098 0,372 0,5 10,8-10® 8,3-10® 48,6 45,6 0,166 0,432 0,6 6,05-10® 5,7-10® 55,3 31,1 0,039 0,258 0,7 4,0-10® 4,3-10® 52,8 29,2 0,012 0,225 0,8 2,4-10® 2,9-10® 39,7 25,9 0,083 0,228 0,9 1,3-10® 1,7-10® 26,7 24,6 0,003 0,119 1,0 0,5-10® 1,1-10® 6,5 20,1 0,018 0,040

е) Данные о сосредоточенных нагрузках на крыло сведены в табл. В.2.

Параметр	Внутренний двигатель		Шасси	Внешний двигатель
М 1	М 3	№ 1	М 3	М 1	>1 3
тк а кГХ	265	345	93,5	Для самолета	221	149
Хсек9’М““1 **1к ® ^	—3,49	—2,60	—1,94	№ 3 нагрузка от шасси объедине­на с нагрузкой	—2,86	-0,59
*1к *м	4,5	5,14	4,5	от внутреннего	9,1	13,8
				двигателя

Таблица В.2

По этим данным была подсчитана первая форма изгибных колебаний крыла для обоих самолетов. Результаты расчета при­ведены в табл. В. З.

Значения инерционных коэффициентов и собственной частоты первой гармоники изгибных колебаний со і даны в табл. В.4.

В.2. ФОРМУЛЫ ДЛЯ КОЭФФИЦИЕНТОВ УРАВНЕНИЙ (3.102) И ИХ ЗНАЧЕНИЯ ДЛЯ РАССМАТРИВАЕМЫХ САМОЛЕТОВ

В табл. В.5 приводятся формулы и значения коэффициентов тех членов уравнений (3.102), которые обусловлены изгибом кры­ла. Значения остальных коэффициентов даны в табл. АЛ «При­ложения А».

В табл. В.5 приняты следующие сокращенные обозначения:

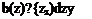
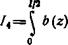1/2

Л = ^ b{z)(zl)dz, о

/3—

где Zi=zcosx;

xK — расстояние между центром давления крыла и центром тяжести самолета: для самолета № 1 хк=0,16 м, для самолета № 3 хк=0,08 м.

2 г,		0,0	0,1	0.2	0,3	0,4	/	0,6	0,7	0.8	0.9	1,0
1х		0,5
і Ш	№ 1	0	0,018	0,053	0,105	0,177	0,274	0,380	0,520	0,650	0,830	1,00
№ 2	0	0,020	0,062	0,112	0,183	0,275	0,378	0,514	0,656	0,837	1,00

Таблица ВА Самолет Mtx-m кГ-сек*-мт кГ’Сек* Mx9-Mtx КГ*СЄК*’М~~* m„=iz кГ-мсек* Afis=Af$t кГ^сек* Ми кГ-секг-мГ~1 "к сект1 № 1 5320 0 685,4 274720 —61,4 285,6 9,4 № 3 5380 0 490 173 000 —1450 244 7,07

Коэффи­ циент	Расчетная формула	Значение для самолета	Размерность
№ 1	№ 3
ь.. к	Мп/т	0,Д29	0,0912	—
ь. к	?еуеСуІіІ»1	0,20	0,395	сек—1
	PevjCy sin у/2/от	0	7,77	сек-1
С.. к	Л*2з//з	-0,013	-0,48	М-1
с. к	PeVXvf4z	0	0,285	М-1»€ЄК-Ї
	РeV]Cy йпу. Хк№г	0	5,5	М-^’СеК-Ъ
еъ	Мз2ІМ33	—0,0046	—0,104	м
ч	VeMulMu	7,5	6,8	Я’сект1
е.. у	Мзі/Мзз	2,39	2,0	• —
е- у	PeVeC°y /і/Мзз	3,7	8,6	сек—1
е. к	PeV^/з/Мзз	2,03	4,85	сект1
	— peVjCy sin ХІ4ІМ33	0	76,3	сек—1

Приложение С

С.1. ДАННЫЕ САМОЛЕТОВ, ИСПОЛЬЗОВАННЫЕ ДЛЯ РАСЧЕТОВ
КОЭФФИЦИЕНТОВ БОКОВОГО ДВИЖЕНИЯ, И КОЭФФИЦИЕНТЫ
УРАВНЕНИИ БОКОВОГО ДВИЖЕНИЯ

В примерах гл. 4 использовались данные о характеристиках бокового движения для самолетов № 1, № 2 и № 5.

При исследовании бокового движения самолета № 1 был вы­бран следующий режим полета: yg=400 м, Ve=360 км/час, ре= =0,120 кГ • мг4 • сек2, Суе=0,62.

Режим полета для самолетов № 2 и № 5 сохранен тем же, что и при анализе продольного движения («Приложение А»). Све­дения о передаточных числах автопилота приведены в табл. С.1.

Таблица С.1 Самолет ‘т ч сек ‘т . ‘* /. ф сек № 1 0,4 0 0.9 0,2 0,6 0,9 № 2 1,0 0,35 0 0 6,0 : 2.0

Коэффициенты уравнений бокового движения даны в табл. С.2.

		Самолет			Самолет
Коэффи­ циент	М 1	J* 2	М 5	^Коэффи-; цчент	№ 1	№ 2	М 5
	0,11	0,116	0,137	‘э	3,9	22,4	15,1
*7	0,098	0,0394	0,0506	п?	1,16	17,3	3,78
	0,775	31,8	3,4	п. 7	-0,04	0,048	0,0053
1. 7	1,9	2,5	4,23	лф	0,32	0,385	0,33
V	0,51	1,41	1,0	пн	0,785	5,74	1,72

Таблица С.2

С.2. ВЫРАЖЕНИЯ ДЛЯ КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ,
ОПРЕДЕЛЯЮЩИХ ПАРАМЕТРЫ БОКОВОГО ДВИЖЕНИЯ
ПРИ ВОЗДЕЙСТВИИ ПОРЫВОВ ВЕТРА

В формуле (4.1):

<h = +

а2=l-k?+п — + + я„, (С 1}

в,—Vt‘S’Vs+ty1?’

h=k^ — Мф), (С 2)

*Зв*р (Ц Яф — *ф ) +/ф Яр — /?Я — . )

В формуле (4.3):

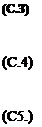^1 — ^ф Яр.

В формуле (4.4):

rfo== Яр,

В формуле (4.6):

ео=*т —Я{,

«і“ V**

/і—)

/2=V* +лз — 1

В формуле (4.8):

го=Лф,

В формуле (4.10):

«і=«і+^9+/фл„,

а2=а2“Ь^-| Uf лн +1 4(^р+лф;+*/»)+

4”/ф Лн (^р + tj ) +/фЛн.

«»—®з4~^ 4/ф лн^р + *т’ 4^рлф + *{ ^э/фЛи +

+*-/э (^р+яф)+*■/»/ф лн+^ 4лр+гф4л^ +
+/фЛ и (^р + ^ )+/ф лнЗД _/тля*ф>

«4 = 04 + ^ 4/фЛн^р + */э/ф пнк& +

+ ija (£рЛф + /фЛн + лв) + г’ф4 (^рл-| +/тля) +

+ /ф«Н^^ + /ф лн^р /ТЛЯ (^р ^рУф )»

«5=гф^э (£j«p 4" Vt71") 4” /ф«н (&j/p+v»*?);

&о“4)~^р»

6i = 6l4- ^p (*f 4 + /ф лн)»

*2=62 + /9 (/фЛ„Лр — Ap/fy + Лр) + /^p +

+ /ф Лн^р^ +/фЛнЛр,

4,= *f фЛн^р + £|4 (/ф ли*р + ^рлф + лр) 4*

+ /флн£/р + ^ф4^рлф ~"/,лн(^ф +^р)4-/фля^ ’

В формуле (4.12):

с0==с0=;р.

^1 = ^1 + У^Ф Лн+

^2==^ф^»Лр4′ УфЛн^р*
d[—dl + Ijip ^2=^в^р f

В формуле (4.15):

е’0=е0=*т-л-,

^=^+/фМт-/т«н,

^2=

В формуле (4.16):

/І=/і + ДЛн.

/^2=Х2“Ь f Ч н^р”Ь fоР’Л — В формуле (4.17):

" ^=£о=Яф.

С. З. К ВЫВОДУ ФОРМУЛЫ (4.27)

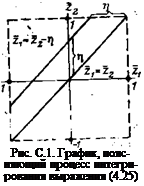На рис. С.1 показан квадрат, внутри которого должно быть проведено интегрирование выражения (4.25). Первый интеграл берется по переменной zj, но так, что­бы независимая переменная r=Z2—z осталась постоянной. В этом случае функцию /?. (V. T, л) при вычислении интеграла (4.28) также нужно считать константой. Пределы интегрирования выражения (4.28) поясняются рис. С.1.

Если нижний предел есть Zi=—1, то при Т) = const верхний предел должен быть 1—і). Для таких пределов инте­грирование при положительных значе­ниях т| включает только верхнюю часть отадрата, лежащую над диагональю Zi=z2. Интегрирование при отрица­тельных значениях г), т. е. в нижней ча­сти квадрата, лежащей под диагональю, даст тот же результат. Поэтому при переходе от (4.25) к. (4.27) постоянный множитель в знаменателе уменьшается в два раза.

нис. с.1 поясняет также переход к пределам 0 и 2 в формуле (4.27) вместо пределов —1 и +1 в (4.25). В последней формуле интегрирование должно проводиться по 2г, а в (4.27)—по т|. При 2i=const переменная т) в пределах квадрата изменяется от О до 2 при изменении г2 от —1 до +1.

С.4. ОПРЕДЕЛЕНИЕ ФУНКЦИИ е (г) ДЛЯ СЛУЧАЯ
РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ ПОДЪЕМНОЙ СИЛЫ ПО РАЗМАХ*

КРЫЛА

В этом случае Ьг=Ьл и из (4.24) получаем

(С Л 5)

Для определения е(г) необходимо найти вращательную про­изводную т’рс. . При вращении крыла с угловой скоростью ю* элемент крыла dz, отстоящий от плоскости симметрии на расстоя­нии 2, получает приращение угла атаки za>xIVe. Это приращение угла атаки создает подъемную силу

dY=Cy^-ba-^-dz (С. 16)

У е 2

и момент относительно ОСИ X

dMx— —dYz— — Cyzbadz. (CM)

Из (С. 17) получаем выражение для момента всего крыла:

(С.18)

* О

т * — X

2V* «, S —- ЩХ=—- — / х 6

На основании (С.18) определяется безразмерная вращательная производная:

Подставляя значение т“* из (С.19) в (С. 15), окончательно получаем

е(2)=6г. (С.20)

С.5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ФОРМИРУЮЩИХ ФИЛЬТРОВ
ДЛЯ ПОЛУЧЕНИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ ПАРАМЕТРОВ
ДВИЖЕНИЯ. ОБУСЛОВЛЕННОГО ГРАДИЕНТОМ
НОРМАЛЬНОГО ВЕТРА ПО РАЗМАХУ

а) для самолета № 1:

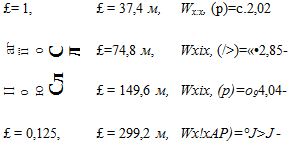1 + 0,25/>;+0,01/>2 ’

0,48 — И0,0554/1 1 + 0,38р + 0,025р2 ’

0,3 + 0,0872р 1 + 0,08р + 0,0975/>2 ’

0,173 + 0,12р 1 + 1,24/> + 0,237/>2 ’

*=0,0625, 1=598,4 *, Г, и, (rt=.,8,08 , ,

*=0,03125, i= 1194,8 48 «V, (,)=<■.! 1,4-^ •

б) для самолета № 2:

А=0,25, £=38,4 м, Wx, x,(p)=«w4,82—————- 0.3 + °,009/?———— ,

£=0,125, £ = 76,8 м, Wx, Xx (p)=am6,8 °’173 + 0,0123/> ,

’ ’ ‘w 1 + 0,128р + 0,00251/12 ’

£ = 0,0625, £=153,6 ж, Wx/x, (/>)«= a,9,64 °’095±^00361^- ,

’ ‘ ’ уу, 1 + 0,099/1 + 0,00153/)2 ’

£=0,03125, £ = 307,2 м, Wx, Xl (/>)=aw13,6- °’°53 + 2:0103Р

’1 ‘ ‘ w 1 + 0,325/1 4 0,00797/i2

£ = 0,015625, £ = 614,4м, Wxlx, (/?)=0^,19,28 °-0282+О’033^ , .

Х1Х, КУ’ w 1 + 1,48р + 0,064/12

С.6. ВЫВОД ФОРМУЛЫ (4.33)

Формула (4.33) получается из (4.31) после подстановки выра­жений (4.28) и (4.32) для равномерного распределения подъем­ной силы по размаху. В этом случае согласно (С.20) е(г) = 6г и из (4.28) следует, чт. о

Г(Ч)=6(4 —б-ri-f і]3). (С.2і)

Перейдем к анализу выражения (4.32). Применив подстанов­ки VeT=|, fa/Ve=X, bx/2=% и использовав формулы (4.29) и

(1.13) , из (4.32) получим

м J ———

Р(К х)=°1 1—^ У¥+Ц е~Т **l’dl (С.22)

Для приведения интеграла (С.22) к табличному вводим но­вую подстановку |=х sh t; тогда

di = xchtdt, W-f-х2=хс^^-

С учетом этих соотношений из (С.22) получим

ОО 1

9 г sh /— — у х eh / г v 1

Р(К х)~°«« ^ е £ 1—~ ch /] ch tdt.

Обозначим iX%/A =sh a, x/^L=ch а,

где Л = -^-V 14-v2=-^-Kl+v2, £=///..

С учетом этих обозначений из (С.23) следует

оо ОО

Р(К x)=4z J ‘"<<+«) сь/л-оі^. ^ g-д ch (<+«)at. (С.24)

—оо woo

Наконец, последняя подстановка /+1а=« приводит (С.24) к виду:

00

Р( x)=°lx J e-Acb*ch(u—a)du —

~Я™~їГ ^ Є“ЛсІ,“с1і2(а — a)du=al>(/1 — /2), (C.25)

/t=X ^ e“’Ache(ch«ch«—bh asha)tf«=xch« J e~A ch “ch и du,=

WOO woo

oo

—2x ch a ^ erA ch “ ch и du—Ki (A), (C.26)

где /Сі(Л) —модифицированная функция Бесселя второго рода первого порядка;

00 во

/2=— [ -а сь«11 і ch 2(а — а)1 du=-£- ^ e-Aeh“du— 4L і 2L J

— оо О

+ — jf ch 2а J erA ch “ ch 2udu=^- 1К0 (Л) + ch 2aK2 (Л)], (C.27)

где Ко(Л) и Кг (Л)—модифицированные функции Бесселя вто­рого рода нулевого и второго порядков. Применяя для Кг (Л) рекурентные формулы, получим

(С. 28)

Подстановка в (С. 25) значений /t и /2 из (С.26) и (С.27) дает

4 ^“^{-^K,[fvT+5]+2^Kl[fV7+5].

(С. 29)

Подставляя значения Г(ц) из (С.21) и P(v, т)) из (С.29) в

(4.31) , получаем

•40“)= (‘з^) ~ J(4 — б71 ~f~ 713)

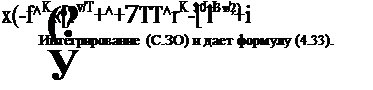* 8яУ? X

Приложение D

ОБЩИЕ СВЕДЕНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТИ,
МЕТОДИКЕ ИЗМЕРЕНИЯ СЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ СКОРОСТИ
ВЕТРА И ОБРАБОТКЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Данные экспериментов показывают, что в большинстве слу­чаев распределение мгновенных значений скорости ветра или любых параметров движения самолета при полете в турбулент­ной атмосфере с достаточной для практики точностью подчи­
няется нормальному закону (закон Гаусса). Плотность распре­деления вероятности в этом случае определяется выражением

/С*)——— l—e 2” , (0.1)

а У 2п

называемая нормированная ности /(*)=

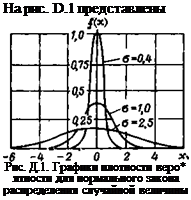графики плотности распределения вероятности для трех различных значений а в предположении, что т=0. Если т отлично от нуля, то соответствующий график смеща­ется по оси абсцисс на величину т. Графики на рис. D.1 показыва­ют, что чем больше о, тем болбе вероятны значительные отклоне­ния случайной величины от ее математического ожидания.

Чтобы привести выражение для плотности распределения ве­роятности случайных величин с различными о и т к единой фор­ме и затем использовать для рас­чета таблицы, применяется так плотность распределения вероят-

Уъ.

где /= -———— аргумент табличной функции.

О

Вероятность того, что значение случайной величины будет на­ходиться в интервале Х — х2, определяется интегралом от плот — ности распределения вероятности, т. е. функцией распределения вероятности.

При нормированном распределении эта вероятность для интервала t-f-/2 определяется выражением

Ф(/‘, *2)=JL^ 2 dt.

где

Выражение (D.3) носит название функции Лапласа или инте­грала вероятности.

В табл. D.1 приведены значения интеграла вероятности (D.3) в функции /2 (в предположении, что /і = 0).

Таблица D.1

j р

Значения интеграла вероятности Ф (<,) = —— е 2 dt

ZJt,)

О

и	* <*.>	12	ф (<-•)	и	Ф (/,.)
0,00	0,0000	0,70	0,2580	1,50	0,4332
0,05	0,0199	0.75	0,2734	1,55	0,4394
0,10	0,0398	0,80	0,2881	1,60	0,4452
0,15	0,0596	0,85	0,3023	1,65	0,4505
0,20	0.0793	0,90	0,3159	1,70	0,4554
0,25	0,0987	0,95	0.3289	1,75	0,4599
0,30	0,1179	1,00	0,3413	1,80	0,4641
0,35	0,1368	1.05	0.3531	1,85	0,4678
0,40	0,1554	1,10	0,3643	1,90	0.4713
0,45	0,1736	1,15	0,3740	1,95	0.4744
> 0,50	0,1915	1,20	0,3849	2,00	0,4772
0,55	0,2088	1,25	0.3944	2,50	0,4938
0,60	0,2257	1,30	0,4032	3,00	0,49865
0,65	0,2422	1,35	0,4115	4,00	0,499968
0,67	0,2481	1,40	0,4192	4,50	0,499997 ,
0,68	0,2517	1,45	0,4265	5,00	0,49999997

С помощью табл. D.1 можно найти вероятность того, что зна­чения случайной величины, математическое ожидание т которой равно нулю, окажутся в некотором интервале ±х2. Табл. D.1 составлена для интервала 0 —t2, поэтому нужно воспользоваться соотношением

| f{t)dt=2

т. е. при подсчете искомой вероятности необходимо удваивать значения Ф(*2), полученные по табл. D. I.

Величина [1—2Ф(*2)] дает вероятность выхода случайной величины за пределы интервала ±х2. Результаты расчетов све­дены в табл. D.2, где интервалы выражены в долях а.

Таблица D.2 Хг /я 2Ф(<*) 1-2Ф (/,) Хг и 2Ф (/я) 1-2Ф (t%) в/2 1/2 0,3829 0,6171 2 3 2 0,9545 0,0455 ф 2/3 0.5000 0,5000 3; 3 0,9973 0,0027 9 1 0,6827 0,3173 4з 4 0,999938 0,000062

Данные, приведенные в табл. D.2, показывают, что около 32% всех значений случайной величины будут превосходить ± о, около 4,5% значений будёт превышать ±2а и лишь около 0,3% значе­ний случайной величины выйдут за пределы ±Зо. Следовательно, можно считать, что практически все значения случайной величи­ны попадают в интервал ±Зо. В этом и заключается так назы­ваемое «правило трех сигм». Из «правила трех сигм» вытекает способ приблизительной оценки среднеквадратичного значения случайной величины: это значение принимается равным одной трети от наибольшего из известных значений. Разумеется, такая оценка является довольно грубой.

При полете самолета в неспокойном воздухе как возмущаю­щее воздействие (скорость ветра), так и значения параметров, описывающих движение самолета, являются случайными функ­циями времени. Случайной называется функция, реализация ко­торой в результате опыта имеет случайный характер, т. е. не может быть предсказана заранее.

Рассмотрим только один класс случайных функций, который имеет наибольшее значение в большинстве задач динамики поле­та в неспокойном воздухе,— стационарные случайные функции. Случайная функция называется стационарной, если все ее веро­ятностные характеристики (определяемые ниже) не зависят от времени. Математический аппарат стационарных функций срав­нительно прост, и расчеты с использованием этого аппарата вы­полняются довольно быстро.

Дополнительным ограничением, накладываемым на рассмат­риваемые ниже стационарные случайные функции, является допущение о том, что эти функции обладают эргодическим свой­ством. Случайная функция обладает эргодическим свойством в том случае, если вероятностные характеристики, полученные осреднением по времени одной реализации (на достаточно боль­шом интервале наблюдения), близки к характеристикам, полу­ченным осреднением по множеству реализаций (при фиксирован­ном времени).

Основные вероятностные характеристики стационарной слу­чайной функции x(t), обладающей эргодическим свойством, определяются следующими выражениями.

Математическое ожидание или среднее значение

т

x(t)= lim ——- x(t)dt. (DA)

при Т-+0О ZJ J

— г

Дисперсия или средний квадрат функции г

•*о(0=°*=Нт ~ [ *o(f)dt, ‘ (D.5)

Т-+ во J

—г

где л:0(^)=л:(/)—л:(/) —центрированная случайная функция.

Далее будут рассматриваться только центрированные случай­ные функции, поэтому для удобства индекс в обозначении этих функций будет опущен.

Корреляционная функция, характеризующая степень связи между значениями случайной функции в моменты t и t+т, равна:

г

/?, (т)=[42](/).*(/-И)=Нт —г x(t)x(t+v)dt. (D.6)

Т-+00 2 Т J —7*

Из сопоставления формул (D.5) и (D.6) вытекает, что

tf,(0)=£. (D.7)

Прямое преобразование Фурье корреляционной функции дает спектральную плотность случайной функции’"

ОО 00

Sx (ев)=— f Rx (-с) е~^штйх=— [ Rx (х) cos шх rfx. (D.8)

Я J Л J

— 00 О

Спектральная плотность характеризует распределение по час­тотам мощности случайной функции x(i). Так как мощность не может быть отрицательной, то и спектральная плотность являет­ся положительной функцией во всем диапазоне частот от 0 до ±оо. Если известна спектральная плотность случайной функции, то, применяя к ней обратное преобразование Фурье, получим корреляционную функцию

ОО ОО

Rx (-с)=-І — J 5 (ш) elatdw = ^ 5 (о>) cos шт d<о. (D.9)

— оо О

В формулах (D.8) и (D.9) замена нижнего предела интеграла

на нуль (вместо — оо) возможна благодаря тому, что корреляци­онная функция и спектральная плотность являются функциями четными. Сравнение формул (D.9) и (D.7) приводит к следую­щему соотношению:

Ox— f (ш)

Аналитические выражения для корреляционных функций и спектральных плотностей случайных стационарных процессов могут быть самыми разнообразными. В качестве примера рас­
смотрим характеристики случайного процесса, называемого «бе­лым шумом» или «абсолютно случайным процессом». Спектраль­ная плотность такого процесса постоянна во всем диапазоне частот, т. е.

Sa(a) = Sa (0) = Const.

Формула (D.11) поясняет происхождение термина «белый шум». Действительно, приближенным аналогом такого случай­ного процесса является «белый свет», в видимом спектре которого содержатся колебания разных частот с одинаковой амплитудой.

Корреляционная функция «белого шума» может быть полу­чена по его спектральной плотности путем применения формулы (D.9), что дает

(£>.12

Формула (D.12) поясняет происхождение второго названия рассматриваемого процесса — «абсолютно случайный процесс». Корреляционная функция типа 6-функции указывает на отсут­ствие корреляционной связи. между любыми сколь-угодно близ­кими друг к другу значениями случайной функции.

Необходимо подчеркнуть, что случайный процесс типа «бе­лого шума» является математической идеализацией, так как физически такой процесс точно реализовать нельзя. Дисперсия этого процесса, как это следует из формулы (D.10), будет бес­конечно большой. Следовательно, и мощность, необходимая для создания такого процесса, также бесконечна. Несмотря на это, в тех задачах, где спектр случайного воздействия значительно пре­восходит полосу пропускания частот исследуемой системы, с успе­хом можно заменить реальный спектр «белым шумом».

Перейдем к рассмотрению методики измерения на самолете случайных составляющих скорости ветра. Как само это измере­ние, так и обработка полученных результатов являются доста­точно сложными и трудоемкими задачами.

Основными параметрами, подлежащими измерению при опре­делении вертикальной и поперечной случайных составляющих ветра, являются углы атаки и скольжения соответственно. Для определения продольной составляющей используется измерение пульсации полного давления на входе приемника воздушного дав­ления. Однако на результаты этих измерений существенное влия­ние оказывают угловые и линейные перемещения самолета.

Учитывая кинематические соотношения, получаем следующие формулы для определения каждой из составляющих истинной скорости ветра при измерении их на самолете: для продольной составляющей

для вертикальной составляющей

для поперечной составляющей

®.(0=V^-h)+s(n2 + y)dt+ly^-lx-^-. (ОЛ5)

В этих формулах, кроме уже известных обозначений, дополни­тельно введены следующие:

«ф. Рф — углы атаки и скольжения, измеряемые с помощью флюгера; эти углы считаются положительными, ес­ли флюгер отклоняется по часовой стрелке относи­тельно осей г и у соответственно; пх, пу, пг — составляющие перегрузки по связанным осям, изме­ряемые с помощью акселерометров, которые счи­таются установленными в центре тяжести самолета;

Длу — отклонение нормальной перегрузки от значения,

N равного единице;

1Х, — расстояние от места установки флюгера до центра

тяжести самолета, отсчитываемые вдоль продоль­ной и нормальной осей;

V — воздушная скорость самолета, измеряемая прием — _ ником воздушного давления;

V — среднее значение воздушной скорости.

Формулы (D.13)— (D.15) справедливы для небольших откло­нений параметров от исходного режима прямолинейного горизон­тального полета с постоянной скоростью.

Углы атаки и скольжения замеряются либо флюгером, либо специальным приемником разности динамических давлений, обусловленной несовпадением продольной оси этого приемника с направлением потока набегающего на самолет воздуха. Флюгер или приемник разности динамических давлений потока устанав­ливаются на штанге перед носком фюзеляжа. Длина штанги должна составлять не менее 1,5 диаметра фюзеляжа, что обес­печивает малое искажение невозмущенного потока на ее кон­це [48}. Кроме того, штанга должна иметь значительную жест­кость. Собственная угловая частота штанги должна быть больше частоты /с*, т. е. наибольшей частоты изучаемого процесса, ко­торая еще представляет интерес.

Реализации случайных составляющих скорости ветра, полу­чаемые на основании данных измерений и расчетов по формулам (D.13) — (D.15), подлежат дальнейшей обработке с целью полу­чения корреляционных функций или спектральных плотностей этих случайных процессов.

Частота f с определяется формулой (D.22), приводимой ниже.

При определении корреляционных функций и спектральных плотностей для случайных стационарных процессов на основании экспериментальных данных возникает целый ряд методических погрешностей. Эти погрешности обусловлены двумя причинами:

1) ограниченной длиной реализации;

2) заменой непрерывной функции п дискретными значениями.

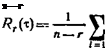Возникает необходимость оценки указанных погрешно­стей и выбора такой методики обработки данных эксперимен­та, при которой погрешности были бы невелики. Метод ре­шения поставленной задачи разработан Тюкеем [46]. Тео­ретическое обоснование метода можно найти в работе [35].

При обработке реализации случайной функции получаем п значений хи расположенных на равных интервалах Д/. По фор­муле

г, г=0, 1, 2т (Ш6)

определяются т ординат корреляционной функции. Значение т находится по формуле

(0.17)

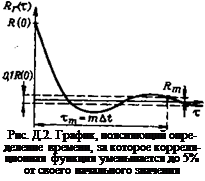
где Ттах — время, за которое корреляционная функция умень­шается до значения |/?т| г^0,05/?г(0) (рис. D.2). Затем определяются предварительные значения ординат кри­вой спектральной плотности по формуле

где

Наконец, определяются уточненные (осредненные) значения ординат кривой спектральной плотности (46]:

<S0(«>)=O,5Z0+O,5Zlf

Sr(u>)=0,25Z, r_i+0,5Zr-f0,25Z,,+J, r=l, 2,…, m — 1, ^«(«)-0,5Ія_і+0,Иж.

248

Из этих выражений следует, что полоса осреднения для каж­дой ординаты равна 2Д<о, где

Дш=т/тД/. (D.20)

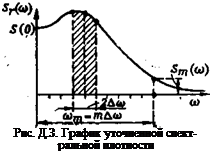В результате расчета получаем /и+1 значений спектральной лотности (рис. D.3), расположенных на интервале Дю. Послед — ее выражение показывает, что чем больше т, тем выше разре­шающая способное ь по частоте в проведенном расчете (интер­вал At определяется харак­тером реализации и изме­няться не может). Но с уменьшением Д© уменьшает­ся и полоса усреднения, что приводит к снижению ста­тистической достоверности полученного значения.

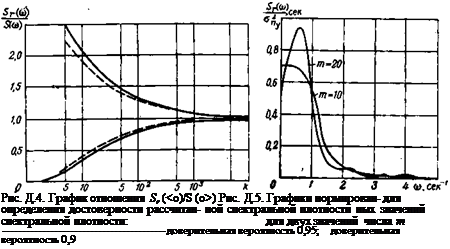
Тюкей установил, что статистическая достовер­ность, определяемая дове­рительной вероятностью с помощью отношения рассчи­танных указанным выше способом значений ординат спектраль­ной плотности 5Г(«>) к истинным значениям этих ординат S(<o), подчиняется закону %2-распределения. Параметром в этом зако­не является число степеней свободы

£=1,6 njm. (£>.21)

График отношения Sr(<o)/S(«>) в функции аргумента k с до­верительными вероятностями 0,9 (пунктир) и 0,95 (сплошная линия) приведен на рис. D.4.

Этот график показывает, что для получения отношения 5r(©)/S©, мало отличающегося от единицы, необходимо иметь значительный аргумент k, что возможно за счет уменьшения т (при данном п) или за счет увеличения п (при данном т).

Для иллюстрации основных положений изложенного метода приведем в качестве примера графики спектральной плотности, рассчитанные по этому методу (рис. D.5). Эти графики относят­ся к спектральной плотности перегрузки, замеренной на самолете в условиях очень интенсивной турбулентности. Среднеквадратич­ное значение перегрузки апу=0,49. Так как длина реализации была небольшой, то удалось получить небольшое число дискрет­ных значений перегрузки (п=200). На рис. D.5 представлены графики, соответствующие числам т= 10 и т=20. При т= 10 кривая получается более плавной, но из-за малой разрешающей способности по частоте отдельные особенности функции спект­ральной плотности исчезли. При т=20 разрешение по частоте вы-

ше, появился существенный пик на частоте со«1, но сглаживание и достоверность графика существенно ухудшается.

Из приведенного описания метода Тюкея вытекает следующий порядок обработки экспериментальных данных для получения значений спектральной плотности с требуемой статистической до­стоверностью.

1.
По характеру реализации определяется высшая существен­ная частота fc таким образом, чтобы на участке спектра, относя-

щемся к более высоким частотам, содержалась пренебрежимо малая часть мощности исследуемого процесса. Свяжем эту час­тоту с пространственными характеристиками турбулентности:

шс VeStc 2я"~ 2я ’

где Ve — скорость полета самолета;

йс — высшая существенная пространственная частота, кото­рую при исследовании поля скорости ветра рекомен­дуется брать й«0,1 VeM~l [48].

Полагая, что на периоде, соответствующем частоте /с, должно со­держаться не менее двух оценок случайной функции, из (D.22) находится интервал времени А/, с которым нужно получать дис­кретные значения этой функции:

Д/=—L- = ——5_. (0.23)

2/с VeQe 0,Ve

2. Исходя из ожидаемого (на основании вида реализации) времени тт, за которое корреляционная функция достигает поло­сы 0,05/?,(0), определяется т по формуле (D.17).

3. По требуемым достоверности оценок спектральной плотно­сти и доверительной вероятности на основании графиков на рис. D.4 определяется аргумент 6.

4. С помощью формулы (D.21) определяется число точек я, которые необходимо получить по реализации:

я = 0,6256т.

После этого можно определить общее потребное время, на ко­тором должна быть определена реализация:

tp=nAt.

Если я получается слишком большим, то формула (D.21) по­зволяет подобрать значения кит так, чтобы за счет снижения разрешающей способности и достоверности результатов получить приемлемое число я (исходя из возможностей цифровой машины, используемой для расчетов).

После того, как по приведенной методике получены все не­обходимые данные относительно At, тип, можно приступать к расчетам на основании (D.16), (D.18) и (D.19). Если в резуль­тате расчета окажется, что при априорном определении %т допу­щена существенная ошибка, следует взять новое значение тт, полученное на основании (D.16), и определить новые значения т, я и /р.

Для ориентировки укажем рекомендуемые в [48] значения т и п, которые приводят к хорошим результатам:

m=40-j-60 и я =15004-4000.

В заключение заметим, что описанный метод полезно приме­нять не только для обработки, но и для подготовки и планирова­ния экспериментов по регистрации реализаций случайных про­цессов с целью предварительной оценки продолжительности реа­лизации, обеспечивающей требуемую достоверность результатов.

[1] Эти задачи в данной книге не рассматриваются.

В динамике полета координаты центра тяжести самолета принято изме­рять в земной системе координат xg, yg, zg причем ось xg этой системы сов­падает с направлением полета, а ось yg — вертикальна.

[2] Стратификацией атмосферы называется распределение температуры в атмосфере по высоте, от которого зависит интенсивность процессов конвекции.

[3] форма дискретного порыва считается фиксированной;

2) под действием порыва самолет может только перемещать­ся по вертикали, не меняя угла тангажа;

3) динамические свойства всех самолетов одинаковы.

На рис. 1.9 показана стандартная форма дискретного порыва, используемая для расчета нагрузок. Линейный участок нараста­ния скорости (длины h) называется «градиентным участком». В качестве независимой переменной принимается расстояние х, проходимое самолетом за время t с постоянной скоростью V.

[4] См. «Приложение D».

[5] См. «Приложение D».

[6] См. «Приложение D».

[7] Выражения (1.18) и (1.19) для спектральных плотностей и соответст­вующие им выражения (1.12) и (1.13) для корреляционных функций исполь­зуются Национальной ассоциацией по авиации и космонавтике США [1].

[8] Случаи, когда учитываются размеры самолета, будут рассмотрены при решении конкретных задач в гл. 3.

[9] При увеличении скорости полета того же самолета это пороговое значе­ние скорости ветра становится меньше, а при увеличении масштаба турбу­лентности, удельной нагрузки на крыло и высоты полета — больше.

[10] Если в невозмущенном режиме полет самолета негоризонтален, то опре­деление проекций скорости ветра следует производить в системе координат (связанной с землей), ось х которой направлена параллельно траектории не­возмущенного полета.

[11] В данном случае совпадающего с земными осями.

______ ные оси х и у

[12] Ниже, в гл. 3, будет приведена методика учета нежесткости конструк­ции самолета.

[13] На рис. 2.3 изображен случай, когда b. Vgx и V gy равны нулю.

[14] Исключение составляет § 3.5.

[15] См. «Приложение D».

[16] Выражения для коэффициентов этой и остальных передаточных функ­ций, характеризующих продольное движение, приведены в «Приложении А».

Рис. 3.1. Амплитудные характеристики для угла тангажа (а), вертикальной (б) н горизонтальной (в) перегрузок при дейст­вии вертикальной и горизонтальной составляющих ветра (са­молет № 1). Характеристики, относящиеся к горизонтальному ветру, отмечены штрихом:

/ — самолет с зажатым рулем; 2 — самолет с автопилотом [закон (2.13)];

[18] — самолет с автопилотом [закон (2.14)]

[19] Выражения для коэффициентов передаточных функций (3.13) — (3.19 > приведены в «Приложении А».

[20] Выражения для коэффициентов передаточных функций (3.22)—(3.27) приведены в «Приложении А>.

[21] Значения передаточных чисел автопилота приведены в «Приложении А®

[22] Выражения для коэффициентов передаточных функций (3.28) —(3.33) приведены в «Приложении А».

[23] В этом параграфе предполагается, что автопилот имеет закон управле­ния (2.14), т. е. высотный корректор выключен; использование автопилота с другим законом управлення будет оговорено.

[24] В работе [15] в качестве наиболее вероятного рекомендуется масштаб £=300 м.

[25] См. например, работы [51, 52].

[26] Термином «большой» для краткости обозначается самолет, у которого учитываются эти два фактора (размах и длина).

[27] См. «Приложение А».

[28] Функция ф (0 уже упоминалась в данной главе —см. формулу (3.53) и далее.

[29] В процессе эксперимента определялось среднеквадратичное значение горизонтальной составляющей скорости ветра. На основании гипотезы об изо­тропности турбулентности предполагалось, что среднеквадратичные значения вертикальной составляющей ветра имеют ту же величину.

[30] Значения коэффициентов а/ и ^ передаточной функции (4.1), выражен­ные через коэффициенты уравнений (2.28), приведены в «Приложении С». Там же приведены выражения для коэффициентов всех рассматриваемых ниже ■ередаточных функций.

[31] Напомним, что через р обозначен угол скольжения относительно воздуха.

[32] При условии, что скорость ветра направлена вверх.

[33] Вывод этой формулы приведен в «Приложении С».

[34] Если рассчитываемые угловые величины (у, ф. Р) должны измеряться в градусах, то коэффициент VА следует умножить еще на 57,3.

[35] Если не учитывать нестационарность обтекания крыла.

[36] Данные самолета № 4 и режима его полета приведены в «Приложе­нии А».

[37] Передаточное. число і А имеет размерность градусы (или радианы) угла отклонения руля на единицу вертикальной перегрузки.

[38] Передаточное число kn имеет размерность — градусы (или радианы) угла отклонения закрылков иа единицу вертикальной перегрузки.

[39] Число превышений принимается равным числу пересечений с положи­тельным наклоном реализацией Any (t) заданного значения приращения пере­грузки £.

[40] Все расчеты проведены для жесткого самолета.

[41] Для современных реактивных самолетов с большой тяговооруженностью предположение о постоянстве ускорения очень близко к действительности.

[42] Необходимо указать, что в формулах преобразования Фурье часто ис­пользуются и другие коэффициенты перед интегралами; это обстоятельство следует учитывать при расчетах.